MATH
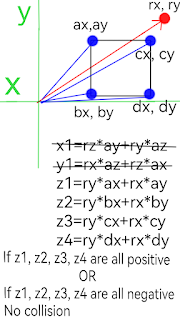
The dot and cross products can be used to detect collisions between rays and AABB's.
This is the cross product version. Repeat the process with another axes pair say x, z. Use the y component formula to get y1, y2, y3, y4. If either views have No collision then No collision has occured.
Using only two axes pairs will fail if x and y are zero. Testing all three axes pairs eliminates this bug.
This is the dot product version, very similar to the cross product version.
Using the cross product and dot product in a grid allows iso-surface extraction. I will call these iso-surfaces "Plancktons".
Marching cubes is basically a lookup table that converts voxels into triangle surfaces. It has 256 possible surfaces. "Plancktons" are derived from a formula and can produce billions of possible surfaces.
To test for a collision between a voxel (sx, sy, sz) and a AABB use this:
if(!((sx-x1>>>6)|(sy-y1>>>6)|(sz-z1>>>6))){ collision=true; }
This will test for a collision with a voxel and AABB at (x1, y1, z1) with dimensions 64x64x64.
A youtuber named Andrew found an interesting equation that creates an animated liquid/gas blob
a=(x-cos(x-a)^2)^2+(y-sin^2(y+b)^2)^2
a range 5 -> 10
b range 0 -> 10
Looks more impressive on Desmos with hundreds of frames of animation.
Create an electric/flame blob by changing a variable.
a=(x-cos(x-a) ^2)^2+(y-sin^2(x+b)^2)^2
a=size of blob
b=animation frame
Drawing an animated equation in canvas.
a>(x-cos(x-a)) ^2+(y-sin(y-b))^2
This is scaled up 32 times. For 1 to 1 scale use:
x=(i&511)/1;
y=(i>>9)/1;
x1=(x-256)-Math.cos(x-a);
y1=(y-128)-Math.sin(y-b);
I usually do not do floating point in rendering but they do not interfere with the array indexes which must be integer values.
Also change the 'a' value upper limit from 4.0 to 5.0 for best results.
This allows for animations that require very little memory.
This animation will be my loading screen.
Change Math.sin(y-b) to Math.sin(y*b) to give this:
LOL!
Relief vs Emboss vs Outline vs Difference of Guassians.
From Math is fun my favourite site.
Linear regression from Math is fun
Combined with the outline of objects interesting information can be extracted. Also a powerful tool for measuring the DEGREE OF SYMMETRY.
Interestingly my statistics book says to limit the r value to two decimal places, but it is the third to sixth decimal place where the most important information is located.















Comments
Post a Comment